A Strategy Used in English Language Arts that Works for Mathematics, Too

By Dianne DeMille, Ph.D. and Jennifer Munoz

Research suggests some reasons students struggle to learn mathematics include: fast pace, reading difficulty, working memory, conceptual understanding, or misunderstanding.

Word problems or problem tasks have always been considered the most difficult part of teaching and learning mathematics at any grade level.

When I taught middle and high school math, I would ask my students, “What job will you have in the future where you will be handed a page full of computations to do or equations to solve?” Sometimes, they would respond with, “Maybe, a math teacher?” Then I’d ask, “Other than being a math teacher?” They were stumped. I would explain the reason we do several problems of similar type is to understand how to get solutions. However, we need to understand how to solve problems or tasks that represent what might occur in daily situations and problems that arise in specialty areas. This is where the mathematics we’re practicing connects to the “real world.”

Reading for comprehension, productive struggle, student reasoning articulation, along with organizing information to determine solution strategies are major components of solving mathematical problems or tasks.

A district-wide Special Education program for secondary mathematics of California Common Core Standards shows success with practical strategies that also work with ALL students. One of the strategies widely used in their program is the “Close Strategy,” often seen in English Language Arts and some other content areas.

While observing a special education class in Algebra, I saw the teacher using the same strategy I had used with all my students in regular math classes. I learned this is a strategy most teachers use, especially in elementary grades, to teach reading. It is the “Close Strategy” that I had never formally learned because it was not part of my training to teach math. We have students who usually had problems in math who are now experiencing mathematics success by using this strategy. As I taught high school students, even in the Honors classes, I used the same strategy.

The Common Core State Standards for English Language Arts directs teachers to have students read informational text with attention to specific detail. Math problems and tasks should be considered informational text.

Professional Development for English Language Arts and other content areas are typically separated from mathematics. This situation does not facilitate a connection of strategies to mathematics. As teachers of mathematics, we often struggle for ways to support students in processing details and solving typical problems and tasks. There are many other strategies that could be adapted for teaching and learning mathematics.

Why not connect English Language Arts with Mathematics and other content areas? Especially when it comes to reading and writing across content. The “close Reading” strategy is just one strategy I have focused on here.

Teachers at all grade levels (K-12) can support their students by using the “Close Reading” strategy. It supports reading difficulties, reading comprehension, slower pace, and conceptual understanding that we know are reasons students struggle. Most problem tasks should be connected to how students read informational text in today’s world.

Have students follow these steps:

1. Read to get a sense of the problem or task.

2. Go back and read each phrase, stop, and verbalize what is meant by that part of the problem. As you read:

• Use “Close” strategies to identify key words, numbers, and questions.
• Use of color, boxes, circles, or some way to see the various types of information is important to share with students (these could the same as used in other content areas)

3. Connect the details, possibly with an equation or diagram – Students may want to create a key for organizing the information (see sample below)

4. Solve the problem

5. Check the solution in the original problem to be sure the question(s) is(are) answered.

All students at all grade levels need to understand this cognitive process. By slowing down and making sense of the steps as they go through a problem, students can be successful.

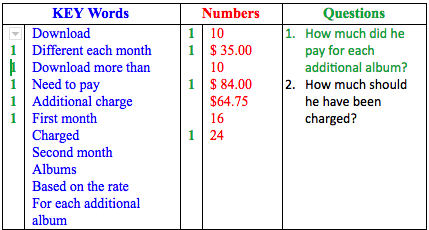
Marvin downloads music albums from an online company. He decides to subscribe to one that allows him to download up to 10 different albums each month for $35.00. If he wants to download more than 10 albums, he need to pay an additional charge. The first month, he downloaded 24 songs and was charged $84.00. How much did he pay for each additional album? The second month, he was charged $64.75 for 16 albums. Based on the rate he paid for each additional album, how much should he have been charged?

Here is a model of how to highlight or underline (we show red, blue, green and underline to represent the process – some find it useful to use a Smart Board or projector on a whiteboard to demonstrate)

• What questions are you asked? (green & underline)
• What are the numbers involved? (red)
• What key words will help you? (blue)

Use “Close” Strategy (Identification of key words may vary)

Marvin downloads music albums from an online company. He decides to subscribe to one that allows him to download up to 10 different albums each month for $35.00. If he wants to download more than 10 albums, he needs to pay an additional charge. The first month, he downloaded 24 songs and was charged $84.00. How much did he pay for each additional album? The second month, he was charged $64.75 for 16 albums. Based on the rate he paid for each additional album, how much should he have been charged?

Organize the information (Pictures and diagrams are useful. Some students may want to use a chart to organize the details)

Use arrows and descriptions to point out various parts of an equation. This will help students visualize how the equation should look and what each part of the equation relates to in the problem. Here is an example for this problem.

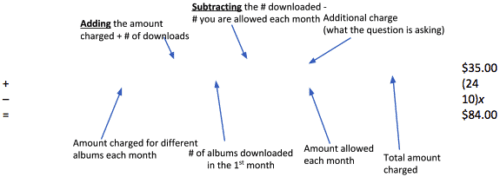
The next step is for students to solve the problem.

The following is a conversation I had with my grandson Timothy when he was in 3rd Grade. He called me for help on a problem his mother, my daughter, did not know how to explain. Timothy was in third grade. My daughter sent me a text with a picture of the problem like this one:

A number made up of the digits 4, 5, and 6 is subtracted from a number made up of the digits 0, 2, 8. The difference is 157. Write out the entire problem.

I asked Timothy to read it to me and was amazed at how well he could read. Then I asked, “Can you tell me what the problem is about?”

I asked him to circle, box, or underline key words, numbers, and the question. Here is an example with my color-coding. Students may identify differently – the important thing is to flush out the important information.

A number made up of the digits 4, 5, and 6 is subtracted from a number made up of the digits 0, 2, 8. The difference is 157. Write out the entire problem.

Timothy, “Something about two numbers and subtraction.”

I said, “You know what? Grandma doesn’t know where to start! I need to slow down and think about the sentences very carefully.”

So, then I asked him to read it again, but to slow down and think about what he was reading. I stopped him after he read “A number made up of the digits.” I asked him, so what is a “digit”? He correctly explained it to me.

Then, I asked him to continue reading. I stopped him again after reading “A number made up of the digits 4, 5, and 6 is subtracted from a number”. I said, “So, what does that part mean?”

Timothy said, “The digits 4, 5, and 6 make up a number and we are going to subtract it from something”

“Ok, now read the next part of the sentence”

Timothy, “a number made up of the digits 0, 2, 8.”

“So, what does that mean?”

Timothy answered, “There is a number made up of the digits 0, 2, and 8 and I’m going to subtract the other number from it.” “Ok, so now what are you going to do?

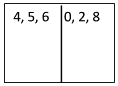He wasn’t sure where to start. So, I suggested we organize the information. We got on FaceTime and I showed him what I wanted him to do. I took a piece of paper and drew a line down the middle to make two sections and shared my drawing. I asked him to make the same drawing and then asked him to write the digits at the top. Then I asked him to write the numbers he could make below the digits in each column. He listed all the numbers on the chart.

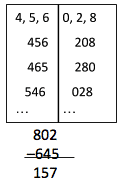I asked, “Which number is subtracted from the other?” He pointed to the columns as he explained correctly. I said, “What will give us a difference of 157?”

He thought for a while and then tried subtracting a couple of numbers. I asked him, “What numbers can you subtract to get ‘7’ for the last digit?” This seemed to give him an idea and then he wrote:

He was so proud of himself and said “Now, I get it! It wasn’t so hard!”

This is the kind of response we want all students to express when we teach them to slow down and take their time. Students need to process every aspect of the problem to get to the result.

This process is not quick, but when they slow down and organize what they can, they can make sense out of the problem.

Author

Further Reading

1. edCircuit – Teaching for Understanding in Math
2. The Atlantic – What Kids Should Know by the Time They’re Done With School
3. The New York Times – Beyond ‘Hidden Figures’: Nurturing New Black and Latino Math Whizzes