Noticing and Wondering

by Jerry Burkhart

Before you read further, spend a few minutes with the image below. What do you notice and what do you wonder?

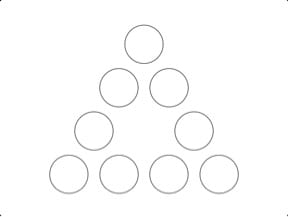
Now take a few moments to reflect.

Were you concerned about anticipating observations or questions I might be “looking for”?

Did you feel comfortable stating or asking “obvious” things?

Did it become easier to generate new ideas as you spent more time with the image?

Was there more to find in the image than you expected?

Do you think you could “improve” at the noticing and wondering process with practice?

How might you use this type of process to support your students’ (and your own) learning?

Check here If you are curious to know how others have thought about this image. As you read further, think back to your experience with the image.

Teaching math differently than you learned it

Research about how people make sense of mathematical concepts demonstrates the need to use students’ ideas as starting points for instruction. Since few of us learned math this way, it may take courage, persistence, and a certain amount of trust to make productive changes in our teaching practice.

So where to start? Clearly, if we are to respond to students’ mathematical thinking, we must first make it visible. By nurturing the habits of observation (noticing) and questioning (wondering) in our math classrooms, we can begin the process of bringing students’ thinking front and center.

The image that began this post is an example of a “noticing and wondering prompt.” Consider two more examples:

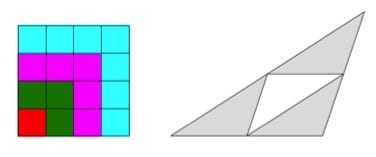
I leave the noticing and wondering to you and your students! As you practice using prompts like these, you gradually learn to recognize—and even create—new examples of images that will elicit interesting ideas from your students.

Unlearning assumptions

It may take time for students to become comfortable expressing their mathematical ideas within such an open-ended format. Both students and teachers may need to unlearn counterproductive assumptions about math arising from earlier learning experiences:

• There is one correct way of thinking.
• Thinking processes always follow rigid rules.
• There is little room for creativity.

However, as you accept students’ responses without judgment, the ideas soon start flowing. Students feed off of and build upon each other’s ideas about images. You gather treasure troves of questions and observations—even for the simplest images. Even ideas that have little to do with math may be valuable, because students are connecting the images to their experience, and you are gaining general insights into how they think.

The next step: prompts and learning goals

After first using noticing and wondering prompts to develop your students’ overall mathematical awareness, curiosity and comfort with sharing ideas, the next step is to bridge the gap between process and content by connecting the prompts to the concepts that you teach. What might these kinds of prompts look like? How can they help your students create mathematical meaning—that is, make sense of mathematical ideas?

A key factor in making sense of math concepts is making connections between them. Spend a few moments with the following prompt for upper-elementary and middle school students. What learning goals could the image address? What might students notice and wonder?

I have used this image to help students develop and compare multiple strategies for calculating the percent of a number. However, students usually begin by producing observations and questions related to concepts and procedures they have learned earlier: fractions, estimation, equivalent fractions, decimals, properties of multiplication and division, and proportions. Notice how this creates the potential to:

• Review and deepen understanding of previously learned concepts
• Connect these concepts to the new learning goals
• Make you aware of students’ misconceptions and insights during instruction
• Help students understand why procedures work
• Support differentiation (because students naturally respond at their level of thinking)
• Support reasoning (by creating opportunities for students to share and compare ideas)
• Develop extensions for students who are ready to explore further (using their “wonderings”)

Notice also how simple many of the images are. Simple prompts tend to encourage a wide range of responses and are likely to be accessible to more students. As discussion progresses, you can modify prompts to zero in on key concepts or to lead the discussion in desired directions.

More examples of prompts that focus on content

Prompts may consist of diagrams, pictures, numbers, or words—anything that leads students to consider mathematical ideas. For many prompts, you can encourage students to make connections to their own experience by asking them to create real-world scenarios that fit the images. Can you imagine doing this for any of the six prompts below? What concepts might the prompts address?

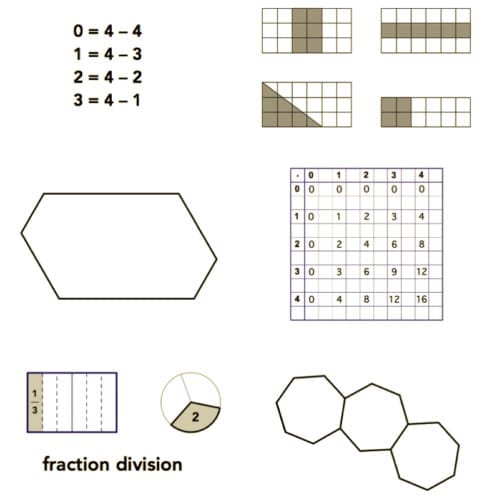
Think about how students might respond to these prompts in different ways and at different levels. Try to imagine how you could modify some of them to make them accessible to more students or to promote further exploration of a concept. Sample responses are available at 5280math.com/noticing-and-wondering/.

Looking ahead

I hope that you can envision how “noticing and wondering” supports positive effective traits and learning skills such as curiosity, confidence, motivation, perseverance, independence, problem solving, creativity, depth of understanding and reasoning. And the process is manageable because you can incorporate it into different aspects of your teaching as you choose—and a little at a time. As you look ahead, consider some of the following ideas.

Places that “noticing and wondering” may fit into your instruction

• Bell-ringers or warm-ups
• Inspiration for new lessons
• Formative assessment
• Enhancing general classroom discourse
• Problem-solving: understanding, exploring, analyzing, and reflecting
• Inspiration for projects
• Differentiation

Building your Practice

• Use prompts to elicit students’ ideas
• Make note of students’ ideas and use them to refine the prompts and your lessons
• Practice using effective questioning and facilitation techniques to focus “noticing and wondering” discussions on your learning goals
• Create, use, and refine your own prompts

Creating your own prompts

Things to consider:

• What is the purpose of the prompt?
• How complex should the prompt be?
• Does it make sense to offer a choice of prompts at different levels of complexity?
• Does it make sense to use a series of prompts to scaffold or extend a concept?

Clearly, there is plenty to learn about building habits of observation and questioning into your math instruction. Fortunately, this learning can happen over time and in the context of teaching and reflection. As you gather observations and questions from your students, you learn more about their thinking and can use this knowledge to enhance lessons each time you teach them. The focus of lesson planning gradually changes from crafting careful explanations to anticipating your students’ thinking and deciding how you will respond.

I would like to invite you to participate in creating a bank of prompts which I have begun at 5280math.com/noticing-and-wondering/. Please contact me at [email protected] to share your images and ideas. Feel free to include information about the grade level, the concepts you are targeting, sample responses from students, or anything else that you think would make the prompts useful for other teachers.

Author

Further Reading

1. Education Week – In Transition to Common Core, Some High Schools Turn to ‘Integrated’ Math
2. The Australian – Australian teachers devise better pathway to maths learning
3. The Atlantic – Why Kids Should Use Their Fingers in Math Class