Teaching for Understanding in Math

by Ed Thomas

Introduction

In a previous article, I indicated that I had an opportunity to survey a small group of adults regarding K-12 math topics they studied when they were in school. I asked them to recall various topics and the degree to which relevance played a role in their math studies. Using a scale of one – 10, where one is least and 10 is greatest, the average response was two. Those survey results showed that most people studied math skills and concepts, without exploring valuable connections between math and the real world.

While I had the group together, I asked them a similar question; “Using a scale of one – 10, to what degree did your teachers help you to understand the math you learned?” Believe it or not, the average response again was two.

There is a difference between learning how to do math and understanding why or how the math works. For example, by the fifth grade, students learn the rule for multiplying decimal numbers;

When multiplying two decimal numbers, place the decimal point in your answer so the number of decimal places right of the decimal point equals the sum of the decimal places, right of the decimal point, in the two numbers you multiplied.

            Note: 4.21 x 2.5 = 10.525

(2 places right of the decimal point + 1 place right of the decimal point = 3 places right of the decimal point.)

But why does this rule work? Most students who learn this rule cannot answer the question why. Sadly, most students are not taught why.

Before dismissing my survey group, I asked them to identify a few things they learned how to do in math, but did not fully understand. Here are some of the more common responses.

Math Topics and Common Misunderstandings

 Grades K – 2

• Why do the whole numbers look the way they do?
• Why do we have to borrow in subtraction? Is there another way?
• Is there a way to be fluent with all the math facts, without having to memorize all the answers?

Grades 3 – 5

• Why do we need common denominators when we add fractions?
• Why do we have to start with the ones column when we add a column of numbers?
• Why is 5 the magic number when rounding to the nearest ten, hundred, or thousand?

Grades 6 – 8

• Why do we need to invert and multiply when we divide by a fraction?
• Why do we use the letter m for slope? Isn’t s a better choice?
• Why does the formula (1/2)(b₁ + b₂)h work for finding the area of a trapezoid?

Grades 9 – 12

• Why do we need the Order of Operations when simplifying numeric expressions?
• Why do we need undefined terms in geometry?
• What makes a parabola curve?

These responses only scratch the surface on math rules, skills, and concepts that students learn but don’t understand. Taking time to help students understand the math they learn increases students’ interest, participation, and achievement in math.

The Five Stages of Teaching and Learning Mathematics

In the year 2000 I developed the Five Stages of Teaching and Learning Mathematics. The Five Stages include:

1) Knowledge (facts, vocabulary, and formulas)

2) Understanding (the ability to explain why math works)

3) Proficiency of Skills (mastery)

4) Application (problem solving and relevance in math)

5) Retention (remembering math over time)

The Five Stages of Teaching and Learning Math can serve as an excellent guide for teachers who want a thorough approach to teaching math. The second stage, Understanding, represents the answer to the question ‘why?’ associated with the math students learn.

When students understand the math they learn, they are more likely to

1) recall important facts, formulas, and vocabulary

2) develop increased proficiencies with important math skills

3) successfully apply math in real-world problem solving tasks

4) retain math longer over time

In other words, relative to the Five Stages of Teaching and Learning Mathematics, Understanding is the one stage that positively impacts the other four stages.

Examples of Teaching Math for Understanding

In our survey, participants offered several math topics that they learned in school, without understanding. The remaining portion of this article addresses one topic from each of the K-2, 3-5, 6-8, and 9-12 grade-level groups. For each topic, the reader is provided some ideas on how to help all students develop important understandings.

Grades K-2

Math topic: Why do the whole numbers look the way they do?

In the earliest days, whole number symbols did not have the smooth curves they have today. Instead, the whole numbers appeared as shown below. Can you see the connection?

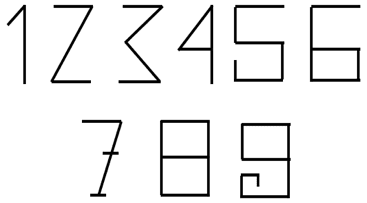
Symbols used for whole numbers were comprised of line segments. Connected line segments form angles. The number of angles in each symbol corresponded to the value represented by the whole number symbol. For example, the symbol for two had two angles. The symbol for three had three angles.   Verify that the number of angles in the other symbols matched the number represented by each symbol.

Grades 3-5

Math topic: Remember the rule ‘5 or higher round up’? Why is 5 the magic number when rounding to the nearest ten, hundred, or thousand?

When students study numbers, the numbers are usually depicted on a straight number line. To help students understand rounding, the numbers can be shown on semi-circles as shown below.

Example 1: Round 53 to the nearest ten.

 The semi-circle of numbers shows that a sliding point placed on the semi-circle left of 55 would fall to 50. A sliding point placed to the right of 55 would fall to 60. The number 55 is the midpoint of the numbers from 50 – 60, and resides at the top of the semi-circle. A point placed at 55 would not fall to either side. For consistency, mathematicians have agreed to round midpoint numbers up to the next ten. In our problem, 53 rounded to the nearest ten is 50.

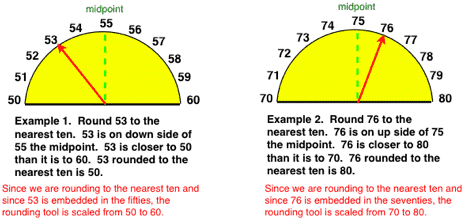
Example 2: Round 76 to the nearest ten.

The semi-circle of numbers shows that a sliding point placed on the semi-circle left of 75 would fall to 70. A sliding point placed to the right of 75 would fall to 80. The number 75 is the midpoint of the numbers from 70 – 80, and resides at the top of the semi-circle. A point placed at 76 would fall to 80. In our problem, 76 rounded to the nearest ten is 80.

Grades 6-8

Math topic: Why does the formula (1/2)(b₁ + b₂)h work for finding the area of a trapezoid?

When students study perimeter and area, they usually begin by investigating rectangles and squares. Note that every rectangle has a base and height. These measures are commonly referred to as length and width. Note that a trapezoid has two bases (top and bottom) and a height.

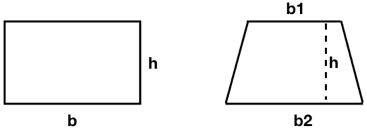
The formula for calculating the area of a rectangle is A = bh.

Consider the area formula of a trapezoid. Similar to a rectangle, the trapezoid has height h.   The difference is the fact that the trapezoid has two bases with measures b₁ and b₂. If, for the trapezoid, we follow the base times height model for the rectangle, which base measure should we use, b₁ or b₂? The best mathematical answer is to use the average of the two base measures b₁ and b₂. How do we find the average? Add the two measures together and divide by 2. Note: multiplying by 1/2 produces the same effect as dividing by 2.

The formula A= (1/2)(b₁ + b₂)h does just that. The formula for area of a trapezoid multiplies the height h by the average of the two bases. This explains the formula for the area of a trapezoid.

Grades 9-12

Math topic: What makes a parabola curve?

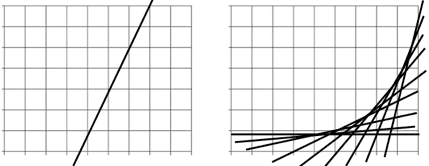
When students study linear equations, they learn that the general form of a linear equation is y = mx + b, where m is the slope. For example, the equation y = 2x + 4 represents a line with slope 2. In a linear equation, the slope remains constant for all values of x.

A linear equation can easily be converted to a quadratic equation (an equation that produces a parabola) by replacing the value m with the variable x.   Thus, the equation

y= mx + b becomes y = xx + b. The equation y = xx + b can also be written y = x² + b.

Comparing the two equations y = mx + b (linear) and y = xx + b (quadratic) shows that the two equations are nearly identical. The only difference is the slope m in the linear equation is a fixed number, and the slope x in the quadratic equation is a variable (constantly changing).

Look at the two graphs below. The graph on the left shows a line that maintains a constant slope 2 throughout. The graph on the right shows lines that have slopes that are constantly changing. The result is a curve. This helps students to understand why a quadratic equation produces a curved line.

Teaching for Understanding and Math Curriculums

Math teachers often teach from curriculums that do not provide direction and information for helping students to understand the math they learn. It is not likely that any of the applications shown above appear on any math curriculum. Nonetheless, these are excellent activities that can help students to develop important understandings of mathematics.

So, what should a math teacher do?

• First, teachers should select and organize the lesson or unit content that follows the Five Stages of Teaching and Learning Math. Typical curriculum content will align well with the Knowledge and Proficiency of Skill stages. Math curriculums often skimp on activities that align with the Understanding and Applications stages. The Understanding stage will remind teachers to prepare math lessons and learning experiences that help students to understand the math they learn.
• Second, math teachers should seek understanding ideas for the math they teach. Teachers can access great ideas through math education conferences, professional development workshops, math education articles and in-house or on-line discussions with colleagues.
• Third, math teachers should show their commitment to understanding math by including understanding questions on their tests and quizzes. A great way to do that is to offer two or three understanding problems on the test, and allow students to choose and write about one. Through choice, teachers can provide opportunities for students to demonstrate their understanding of math.

Summary

In too many classrooms, students learn math words, formulas and routines without understanding them. This can lead to patterns of mathematical mistakes, difficulties with problem solving and short retention spans. Without understanding, students are likely to become frustrated in math and lose interest in their math studies.

Understanding is a key component of the Five Stages of Teaching and Learning Mathematics. Understanding can have positive impacts on the other four stages. Math teachers should include lessons in their units that help students develop important understandings. Strategies for teaching for understanding are available through professional learning events and a variety of published articles and texts.

Author

Throughout his career, Ed Thomas has served in public education as a math teacher, district math supervisor, and math-instruction consultant. Ed earned a Ph.D. in K-12 math education at Georgia State University. His writings span a dozen texts and several articles.   His latest book is Turbocharged Math Instruction; Powerful Instructional Strategies for Great Math Lessons. Ed is a national presenter and has spoken at a variety of education conferences including ASCD, SREB, AMLE, OSII, NCTM, and GMSA. You can find a listing of resources by Ed Thomas at MyEdExpert.com.

1. Ed Week – Math ‘Makes the World More Beautiful’: A Professor’s Advice on Teaching Math
2. Ed Surge – Math Teachers Need Better Professional Development. Here’s a Personalized Approach
3. WBUR – Do We Really Need To Learn Advanced Math? One Professor’s Case For A More ‘Practical’ Approach